El tradicional bautizo de guagua se realiza durante todo el mes de noviembre, "mes de los compadres"; ésta singular tradición arequipeña, parodia el bautismo católico y hace que los amigos estrechen aún más los vínculos de amistad. Se compra guaguas, similar a un bebe como si estuviera envuelto en pañales y no aparezcan los brazos, pero si la careta, cara pequeña de yeso, cuyo rostro es muy hermoso y el gorro es decorado con florcitas si es mujer y si es hombre un gorro de color entero. El bautizo de guagua, es una fiesta donde en forma jocosa y parodiando un bautizo católico se procede a una ceremonia donde, el cura con su sacristán, el papá, la mamá de la guagua, los padrinos que luego serán compadres, así como todos los asistentes como testigos; el cura es el que preside la ceremonia de bautizo y los invitados más chistosos y ocurrentes, previamente disfrazados parodian el ritual, entre bromas, chistes, anécdotas, cuentos y chismes, de cómo los padres hicieron la guagua,en febrero, en que lugar, si alguien los vió, con frases de doble sentido o sentido figurado, cánticos, rimas...echando el agua bendita y pronunciando jaculatorias, maldiciones y bendiciones. Finalizando el acto se procede a cortar en pedazos pequeños para que alcance y coman todos los presentes en señal de aceptación y alegría.
Las siete piezas del tangrames un excelente material didáctico para favorecer entre otras cosas: Orientación espacial, Estructuración espacial, Coordinación visomotora, Atención, Razonamiento lógico espacial, Percepción visual, Memoria visual, Percepción de figura y fondo. Se utiliza también en la psicología, en diseño, en filosofía y particularmente en la pedagogía. En el área de enseñanza de las matemáticas el Tangram se usa para introducir conceptos de geometría plana, y para promover el desarrollo de capacidades psicomotrices e intelectuales de los niños pues permite llegar de manera lúdica la manipulación concreta de materiales con la formación de ideas abstractas. En matemáticas se puede utilizar para introducir conceptos de geometría plana, contextualizar sobre las fracciones y las operaciones entre ellas, pueden comparar y visualizar claramente la relación parte-todo que denominamos fracción. Comprender y verbalizar la notación algebraica, deducir relaciones, fórmulas para área y perímetro de figuras planas. ángulos, distancias, proporcionalidad, semejanza, movimientos..., todas ellas pueden tratarse fácilmente con Descartes.
Para los niños, puede ser una gran oportunidad para acercarse a los conceptos geométricos de líneas rectas, diagonales, rectángulos, cuadrados, triángulos, simetría, etc.
Proporciona una herramienta pedagógica que permite desarrollar diferentes contenidos, no sólo conceptuales sino de procedimiento.
Desarrolla la psicomotricidad y, fundamentalmente, la psicomotricidad fina,así como la percepción espacial.
Desarrolla la destreza manual, la exactitud en la realización del trabajo y la precisión manual.
Relaciona la disciplina de las matemáticas con otras ciencias, como las artes, por ejemplo.
Motiva al niño a ser creativo, ya que puede desarrollar sus propios modelos e investigar la conexión que tiene con la geometría no sólo plana, sino también espacial.
Os recomiendo hacer papiroflexia con ellos ya que es creativo, divertido y económico.
Una pirámide es un poliedro, cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice común, llamado cúpide, que es el vértice de la pirámide.
Elemenos de una pirámide
Los elementos fundamentales de una pirámide son caras, aristas y vértices.
Las caras pueden ser: - Base de la pirámide, que es un polígono cualquiera. - Caras laterales de la pirámide, que son triángulos. Las aristas pueden ser: - Aristas básicas, que son los lados de la base. - Aristas laterales, que son los lados de las caras laterales que no son aristas básicas. Los vértices pueden ser: - Vértices de la base, que son los vértices del polígono de la base. - Vértice o cúspide de la pirámide, que es el punto en el que se encuentran las aristas laterales.
A partir de la superficie de revolución se generan diferentes sólidos que se llamarán sólidos de revolución. Estos cuerpos redondos ode revolución son: la esfera, el cono, y el cilindro . Podemos obtener cuerpos de revolución de lo más variados, simplemente basta con girar una figura plana sobre un eje.
El icosaedro formado por 20 caras que son triángulos equiláteros iguales.
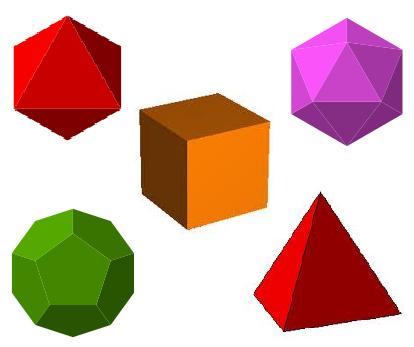
LOS POLIEDROS REGULARES son cinco:
El tetraedro formado por 4 caras que son triángulos equiláteros iguales.
El hexaedro o cubo formado por 6 caras que son cuadrados iguales.
El octaedro formado por 8 caras que son triángulos equiláteros iguales.
El dodecaedro formado por 12 caras que son pentágonos regulares iguales.
Los poliedros regulares son poliedros convexos con todas las caras idénticas que son polígonos regulares y con todos los vértices recibiendo el mismo número de aristas. Solo existen 5 tipos de poliedros regulares: tetraedro, octaedro, icosaedro, cubo y dodecaedro.
ELEMENTOS DE LOS POLIEDROS REGULARES
Los panales de abejas tienen forma de prismas hexagonales
El virus de la poliomelitis y de la verruga tienen forma de Icosaedro
Las células del tejido epitelial tienen forma de Cubos y Prismas
El fullereno (C60 ) cuya forma es un icosaedro truncado.
Los balones de fútbol han estado hechos siempre con 12 pentágonos y 20 hexágonos.
En sus formas naturales, muchos minerales cristalizan formando poliedros característicos
El tradicional bautizo de guagua se realiza durante todo el mes de noviembre, "mes de los compadres"; ésta singular tradición arequipeña, parodia el bautismo católico y hace que los amigos estrechen aún más los vínculos de amistad. Se compra guaguas, similar a un bebe como si estuviera envuelto en pañales y no aparezcan los brazos, pero si la careta, cara pequeña de yeso, cuyo rostro es muy hermoso y el gorro es decorado con florcitas si es mujer y si es hombre un gorro de color entero. El bautizo de guagua, es una fiesta donde en forma jocosa y parodiando un bautizo católico se procede a una ceremonia donde, el cura con su sacristán, el papá, la mamá de la guagua, los padrinos que luego serán compadres, así como todos los asistentes como testigos; el cura es el que preside la ceremonia de bautizo y los invitados más chistosos y ocurrentes, previamente disfrazados parodian el ritual, entre bromas, chistes, anécdotas, cuentos y chismes, de cómo los padres hicieron la guagua,en febrero, en que lugar, si alguien los vió, con frases de doble sentido o sentido figurado, cánticos, rimas...echando el agua bendita y pronunciando jaculatorias, maldiciones y bendiciones. Finalizando el acto se procede a cortar en pedazos pequeños para que alcance y coman todos los presentes en señal de aceptación y alegría.
